Zeven Development

The Fractal Algorithm
Special thanks goes to my son Nathaniel Huygen for beta testing The Fractal Algorithm program and to his contributions to calculating, and simulations of Fractal Periods and Orbits.
 The Fractal Algorithm is 100% free with no trial periods or advertising,
and can be used by companies for demonstration purposes, but we do request
that you send us a photo of when and where it was shown to the public,
so that we can compile a gallery.
The Fractal Algorithm is 100% free with no trial periods or advertising,
and can be used by companies for demonstration purposes, but we do request
that you send us a photo of when and where it was shown to the public,
so that we can compile a gallery.
Fractals are infinitely complex and beautiful, but due to the sheer number of computations required to create these images, it has been a challenge to make it zoom in real time. The Fractal Algorithm is an attempt to achieve this.
There are many fractal programs on the internet, but all have one or more of the following limitations:
- Too slow and some images can take several minutes to even hours!
- Low resolution in a window that won't go full screen.
- Low number of Iterations. The higher the count, the longer it takes.
- Difficult to use with too many shortcut options that end up corrupting the image.
- Uses a GPU if you have the exact one, but does not zoom in very far.
There are also many videos of fractal zooms and animations, but all have one or more of the following limitations:
- Take up too much hard drive space.
- Blurry due to antialiasing.
- Blocky due to compression artifacts
- Quantization artifacts from higher compression rates.
- Lower resolution than full screen display resulting in loss of finer detail.
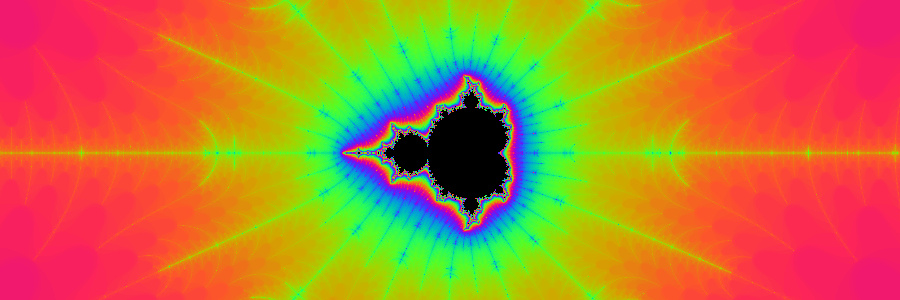
There has to be a much simpler way to calculate fractals quickly so that we can zoom in real time, and at Zeven Development we have found such a way! Only calculate the boundary lines of the fractal! But how is that possible? Let's take a look at the Mandelbrot Set at a zoom factor of 1.0, and at a resolution of 1920x1080 we will call the Home position. The Fractal Algorithm only needs to calculate 7.4% of the total resolution. This is achieved by using another fractal to calculate the Mandelbrot Set called Huygen Lines
Huygen Lines
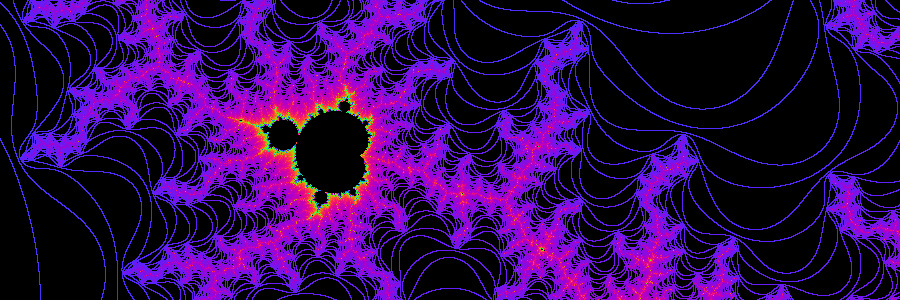
All fractals are bounded by the iteration escaping, eventually approaching infinity. This behavior can be taken advantage of by using Huygen Lines to very quickly find these boundaries and discard all the areas in between, even in the areas of infinity, thus only calculating the boundary lines.

Move your mouse over the image to view additional detail. The bottom half of the fractal is shown normal since it is symmetrical and not calculated. All the areas in white are also not calculated. Look at the area of infinity normally colored in black, it requires the most CPU because it has the highest iteration count, but that area is now mainly white, only the edges are calculated. Another important feature of Huygen Lines is that the higher the resolution you go the less area you have to calculate. This is critical in being able to calculate higher resolutions quickly.
| Resolution | Calculated |
|---|---|
| 800x600 | 12.21% |
| 1024x768 | 10.81% |
| 1280x720 | 9.14% |
| 1366x768 | 8.84% |
| 1920x1080 | 7.40% |
Here is another zoomed in image that only needs to calculate 13.52%.
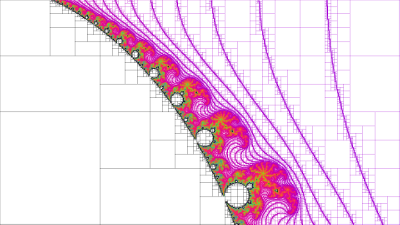
Huygen Lines also lends itself to be highly parallel, resulting in very efficient multiple CPU utilization. So now we have a faster way to calculate a fractal, by only having to calculate the boundary lines. The technique of Huygen Lines is completely different from Successive Refinement that is commonly used in most fractal programs, and is far more efficient in removing larger areas, and does not suffer the image loss associated with chunk size guessing.
Huygen Lines also has a much wider use in other areas such as adaptive image compression and face recognition.
Symmetry
Any Symmetry that is detected is not calculated. Symmetry only helps if the fractal image intersects the axis where y=0.
Cardioid/Bulb, Periodicity And Orbit Detection
In order to view all the detail we need to increase the iteration count, which will slow us down even further, especially on areas of infinity. The Fractal Algorithm on the home screen shown above was generated at 1,000,000,000 iterations, yes one billion, in 46ms on a standard quad core laptop. To calculate the Dragon Julia Set at a resolution of 1920x1080 at one billion iterations it takes only 31ms! How is this possible? By using advanced Cardioid/Bulb, Periodicity and Orbit Detection. As iterations approach infinity patterns will emerge that The Fractal Algorithm can quickly detect and exactly predict the escape. If the fractal image were iterated to the full iteration count they would be identical, not to mention how slow it would be as well.
Dynamic Iterations
When a zoom point has been selected The Fractal Algorithm will pre-calculate the zoom so that it can pre-determine the lowest maximum iteration needed. If you specify a high iteration count for a fractal image there are normally only a couple of points that are in the upper iterations and this quick optimization finds the lowest maximum iteration needed for infinity at the zoom location. This iteration list saves a lot of calculation time with areas of infinity when zooming the fractal.
Hand Optimized Assembly
In order to squeeze every clock cycle out of the CPU, the main iteration loop was written using hand optimized assembly. Both FPU and SSE2 instructions are supported. The FPU does 80-bit double precision iterations and is slightly more accurate, verses the dual 64-bit double precision SSE2 calculations, but the SSE2 will be slightly faster. The additional precision can only be seen near the limits of the FPU. The FPU iteration loop is so efficient that it runs only in the FPU stack.
fld exit // exit = 4.0
fld c2
fld c1
fld x
fld y
mov eax,iterations
IterateLoop:
fld st(1) // x
fmul st,st // x * x
fld st(1) // y
fmul st,st // y * y
fld st(1) // x * x
fadd st,st(5) // (x * x) + c1
fxch st(4) // x
fmulp st(3),st // y * x
fadd st(1),st // (x * x) + (y * y)
fsubp st(3),st // ((x * x) + c1) - (y * y)
fxch st(1) // y * x
fadd st,st // 2 * (y * x)
fadd st,st(4) // (2 * (y * x)) + c2
fxch st(1) // (x * x) + (y * y)
fcomip st,st(5)
ja IterateDone
dec eax
jnz IterateLoop
dec eax // Infinity is -1
jmp short IterateExit
IterateDone:
neg eax
add eax,itertions
IterateExit:
fstp st(0)
fcompp
fcompp
}
Multiple CPUs
The Fractal Algorithm will detect and use all your CPU's for calculating the fractal. The algorithm has been highly optimized for multithreading, with screen updating having the highest priority. In order to minimize thread synchronization requests to the OS, atomic operations have been used instead by using Interlocked Variable Access. If you have a quad core CPU with hyperthreading, then you will have 8 CPU's available for calculating, and if you also enable SSE2, then you can perform two double precision floating point calculations for each CPU at the same time called SIMD, so that's like having 16 CPU's calculating the fractal at the same time. Just because SSE2 can perform two double precision calculations at the same does not mean that you will get double the performance over a single FPU. Due to algorithm parallelism restrictions, and 128-bit memory accesses you will normally see only about a 30% improvement.
Now that we can generate a single fractal image quickly we need to be able to generate at least 30 of them per second. Most fractal images can be generated quickly but more time is needed to calculate fractal images that contain a lot of detail, so another technique had to be created called Huygen Predictors
Huygen Predictors
If you zoom in on a region of the fractal and create a new image, then using the saved iterated states of both images, where they intersect, Huygen Predictors can very quickly and accurately predict additional images. This is an iterated prediction, not pixel enlargement or interpolation. Regions outside the zoomed image where there are no intersection can only be enlarged, but since we are zooming this creates a nice motion blur effect helping in the zoom animation. You will notice in predicted images, areas that contain a lot of detail, changes with every frame and will get the exact same effect if the predicted frame was calculated instead.
Reversible Queues
Fractal images are calculated as fast as possible for zooming in, and are added to the end of a reversible queue buffer. This will allow for a smooth zoom because not all images take the same time to calculate. When the fractal animation has finished zooming in, the queue is reversed allowing the fractal to zoom back out, reusing the previously calculated images. The time gained in the reverse allows the zoom to catch up with its calculations.
Mandelbrot And Julia Sets
At this time only the Mandelbrot and Julia Sets are supported. You can specify any c1 (real) and c2 (imaginary) for the Julia Set, or select from a predefined set of well known Julia's. Other fractals can be easily added and are being explored.

Click to select and magnify any of the above fractal images.
Cache Home Screen
Since we are zooming in and out the Mandelbrot Home position with a zoom factor of 1.0 is cached, so it is only calculated one time for the entire preview.
Video Resolutions/Bit Depths
All video resolutions and bit depths that your video card can do are supported. Why support different resolutions and bit depths? Because this allows you to select the throughput that best meets your computer. At 1920x1080 @30fps that's 248,832,000 bytes/sec, that's a lot of data. Interestingly the fractal calculations are so fast that the limiting factor has now become the video bandwidth from the CPU system memory to the video card memory.
| Resolution | Bit Depth | Bytes | @30fps |
|---|---|---|---|
| 800x600 | 8 | 480,000 | 14,400,000 |
| 1024x768 | 8 | 786,432 | 23,592,960 |
| 1280x720 | 8 | 921,600 | 27,648,000 |
| 1366x768 | 8 | 1,049,088 | 31,472,640 |
| 1920x1080 | 8 | 2,073,600 | 62,208,000 |
| 800x600 | 16 | 960,000 | 28,800,000 |
| 1024x768 | 16 | 1,572,864 | 47,185,920 |
| 1280x720 | 16 | 1,843,200 | 55,296,000 |
| 1366x768 | 16 | 2,098,176 | 62,945,280 |
| 1920x1080 | 16 | 4,147,200 | 124,416,000 |
| 800x600 | 24/32 | 1,920,000 | 57,600,000 |
| 1024x768 | 24/32 | 3,145,728 | 94,371,840 |
| 1280x720 | 24/32 | 3,686,400 | 110,592,000 |
| 1366x768 | 24/32 | 4,196,352 | 125,890,560 |
| 1920x1080 | 24/32 | 8,294,400 | 248,832,000 |
The Fractal Algorithm currently only supports 236 colors, so it will look the same at any bit depth. Why 236 colors? Because the lower ten, and upper ten are reserved for Windows System Palette. The Fractal Algorithm was originally written to take advantage of hardware palette rotation, which was extremely fast, but as newer video cards have come out, they no longer support palletized video modes except through emulation which is slower than the natively supported 16-bit or 32-bit color depths.
DirectX

To achieve the highest video update speed possible, direct video hardware access is performed using double buffer page flipping with DirectX's DirectDraw7. It you have any issues with DirectDraw you can still use DrawDIB (Device-Independent Bitmaps).
Multiple Monitors
The Fractal Algorithm has multimonitor support in it, but it is only available through DrawDIB. Also please be aware that the higher the combined resolution of all your displays, the greater the video memory bandwidth required. On multimonitor tests, the bottleneck was not the fractal calculations, but rather the video updating. All the default fractal zoom points will have to be recalculated to update the Dynamic Iteration lists to match your multimonitor setup. To update the iteration lists, edit each fractal zoom point in multimonitor mode and press 'Enter'.
Color Cycling
To create a cool motion effect, color cycling will rotate the colors. The colors are selected by taking the iteration count modulus 236. The colors are updated for every image displayed and when its waiting to calculate the next image.
Config Dialog
The main config dialog consists of a list of fractal Zoom Points and a list of Color Palettes with configuration options for playback. Here you can select the Zoom Factor and frame rate for all the Zoom Points. In this case one frame is calculated and 29 predicted and displayed every 1000ms or 30 fps. If you have a faster computer change the zoom factor to 2, display every 500ms to display 60 fps. Just press the Preview button and enjoy!
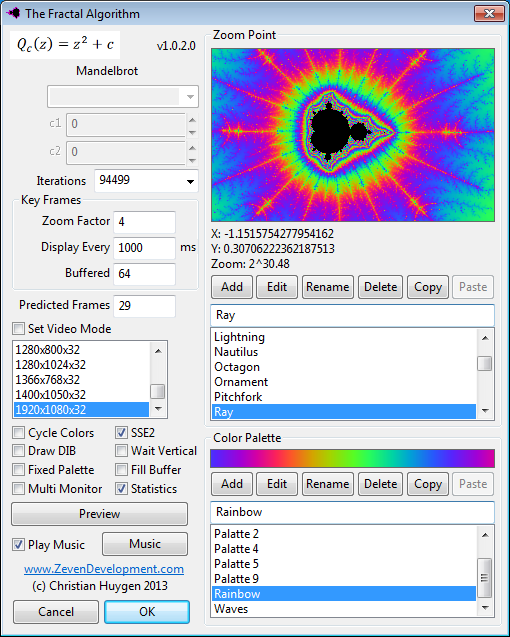
Cut & Paste
Sharing your favorite fractal zoom points and/or palettes is very simple to do. To copy a zoom point, select it and press the copy button, or right click on the preview window and select copy. Using any text editor just paste it in. To add a fractal zoom point, just highlight the text in your editor or web page and copy it. Then press the paste button or right click on the preview window and select paste. It's that easy!
Fractal=Thorns 1 0,0 -1.7837419492892297,-2.0293772219380132e-014,1.09951e+012 90834 41,2,2,2480,3610,3842,185,726,2401,8638,13772,13577,7184,3275,872,3182,11053,29827,44985,31463,3082,10744,31033,62786,61051,24567,11210,32942,1916,3689,10765,26419,61874,7152,1965,2168,2495,2976,4120,7867,15081,39507,68782,90834
Let's add a new zoom point. Highlight the above data and copy it. Then paste it into The Fractal Algorithm by pressing the paste button or right click on the preview window and select paste.
What do all these numbers mean?
Fractal=Name of Fractal Zoom Fractal type; 1 = Mandelbrot, 2 = Julia Set c1,c2 of Julia Set x,y,zoom of Fractal Zoom Point Number of Iterations Dynamic Iteration List
Fractal Editor
To explore the fractal, The Fractal Algorithm has a fully functional editor. Zoom in and out untill you find the location you like and press 'Enter' to select it as another zoom point in your list.

Edit window for the Mandelbrot at the Home position. The Help menu will only appear the first time you edit or press the 'H' key.

Using the mouse move the window to the desired location and press the left mouse button to zoom.
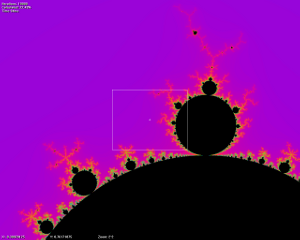
The new point is zoomed in.
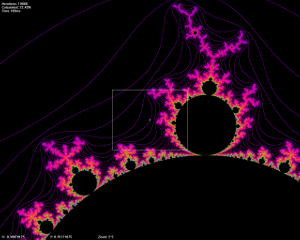
Boundary Lines
To see all the boundary lines that Huygen Lines found, press the 'B' key in the Fractal Editor
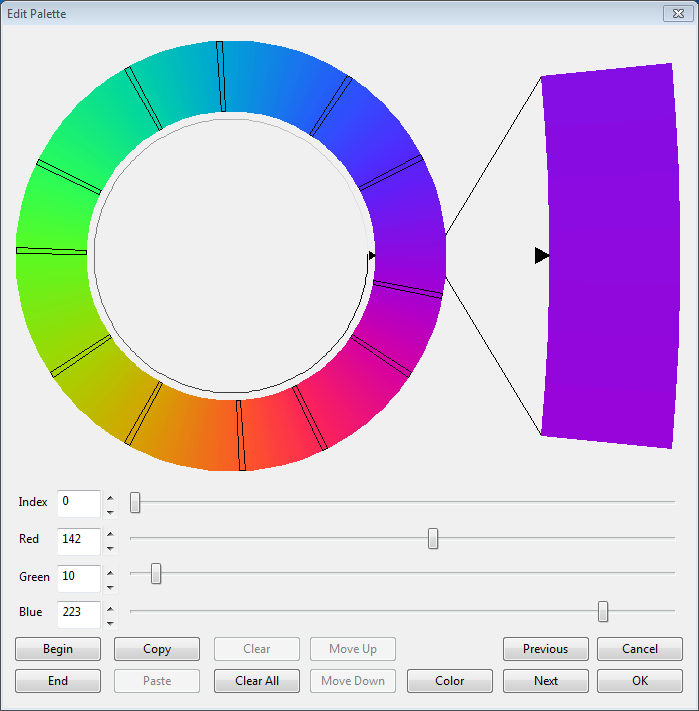
Palette Editor
To quickly create or modify a color palette The Fractal Algorithm supports a full Palette Editor. For the simplest and most intuitive design, a color wheel has been used to represent the color transitions. You can highlight blocks, copy/paste, clear, move and select colors. Selected colors are highlighted in either a white or black outline. Colors in-between are automatically graduated. Click on any color in the wheel or magnification to select the color, or use your mouse wheel to rotate the color wheel.
Music
What is a fractal zoom without your favorite music? A silent fractal zoom, and that's no fun! The Fractal Algorithm plays all different types of music files using MCI so enjoy! Play .au,.snd,.mp3,.wav,.asf,.wma,.mpg,.mid,.rmi,.vod,.dat file formats.
Preview
Watch the currently selected fractal zoom point. Once it is done, it will randomly select another zoom point.
Statistics
To help you interpret what is happening during a fractal zoom, you can display its statistics. Statistics are displayed in the upper and lower left hand corner. Calculating and displaying statistics may slow down your fractal zoom slightly.

What do the statistics display?
- Fractal: Name of Zoom Point.
- Palette: Name of Color Palette used.
- Resolution: Screen Resolution.
- Memory: Amount of RAM used.
- Generated: Total displayed image data. This is the amount of image data that the fractal zoom has generated and displayed.
- Iterated: Total displayed iterated data. This is what would have to be fully iterated to match the displayed fractal zoom.
- Buffered: Number of calculated images buffered.
- Iterations: Current number of iterations.
- Calculated: Current percent calculated for the image after Huygen Lines discarded the rest.
- Time: Current time it took to calculate the image.
- Processors: Number of processors used to calculate the image
- Fps: Frames per second.
- Zoom: Current Zoom Factor.
Save Image
Want to save you favorite fractal image? Use the Fractal Editor and press 'S' to toggle statistics off, and 'Z' to toggle the zoom window off and press the 'Print Scrn' key. You can then paste it into any document or paint program.
Screen Saver
Did you know The Fractal Algorithm is also a screen saver? So impress your friends or co-workers and display your favorite fractals zooms when your computer is idle. The screen saver is already installed by default, just enable it under Personalization in Windows, or click the Windows button and search for 'Change Screen Saver'.
Note: Using the screen saver password option and setting an 8-bit DirectX full screen video mode will default to the desktop resolution and bit depth, because the windows login account does not have access to the task bar. The windows task bar (explorer.exe) needs to be terminated because it is restricting the screen saver from setting the palette correctly.
What's Next?
With all the features and new technologies that have already been development in The Fractal Algorithm, there is always room for improvement. So what's being developed next?
- DirectX 11. DirectDraw has already been depreciated by Microsoft.
- 64bit. Unfortunately only SSE2 will be supported. It will also allow for additional XMM8 - XMM15 register optimizations.
- Additional Windows 8 support.
- AVX Optimization to perform operations on four 64-bit doubles per clock cycle.
- Double Double 30 decimal place floating point arithmetic for deeper zooms.
- Addition of new fractals.
If you have any feature you would like to see in our next version, please contact us and let us know.